컴퓨터의 세계에서는 모두 ON과 OFF, 즉 1과 0으로만 모든 것이 처리된다고 했지? 이것을 수학에서 배운 것으로 표현하기 위해 2진수라는 것을 배웠다.
비트(Bit)란?
2진수 한 개(한 자리)를 컴퓨터에서는 Bit라는 용어를 사용해. Bit는 Binary Digit에서 앞의 2글자와 맨 뒤의 한 글자를 따온거야. Binary는 "2개로 이루어진" 혹은 "2진수의" 뜻을 가진 형용사고 Digit는 "숫자"라는 명사야. 이 틈에 영어 공부도 하니 참 좋네. 2진수가 한 개만 딸랑 있는 경우 1비트, 2진수가 8자리 숫자로 있는 경우 8비트, 이런 식이지.
2진수는 자리 수가 늘어날 때마다 2배씩 커지게 되는데, 이걸 수학적으로 보면 2의 거듭제곱과 같아. 거듭제곱에 대해서 복습하면, "2의 n제곱은 2를 n번 곱한 것"으로 2ⁿ과 같이 수학에서 표시하는데, 컴퓨터 자판으로 글을 쓸 때 제곱수(n)을 위첨자(superscript, 작은 글자를 위에 붙여서 쓰는 것)로 일일이 쓰는 것이 어렵기때문에 2^n과 같이 ^(caret, 꺽쇠)를 이용한다.
예) 2⁴= 2^4 = 2x2x2x2 = 8
2진수 8자리를 가지고 표현할 수 있는 범위는 0b00000000부터 0b11111111 까지인데 이걸 10진수로 바꾸어 보면 0부터 255까지, 모두 256개의 숫자를 셀 수 있어. 사람 손가락이 10개이기 때문에 그런지 몰라도 아무리 공부를 못해도 1에서 10까지는 더하고, 빼거나 기억하는 것이 가능하다고 보면 컴퓨터도 한 번에 기억하고 계산할 수 있는 숫자의 범위가 있어. 다시 말하지만 컴퓨터는 2진수를 기준으로 한다는 것을 잊지 않았으면, 한 번에 8자리 숫자를 처리하는 컴퓨터는 8비트 컴퓨터, 한 번에 32자리 숫자를 처리하는 컴퓨터는 32비트 컴퓨터라고 한다. 8비트 컴퓨터는 CPU가 0~255 사이의 숫자를 읽고 계산하고 할 수 있어. 물론 이것보다 큰 숫자를 계산하기 위해서는 여러 번에 걸쳐서 나누어서 하게 되지.
요즘 쓰는 컴퓨터들은 64비트 CPU를 사용해. 30여년 전에 스티브 잡스라는 사람이 애플이라는 회사를 만들어서 처음 PC를 만들어 팔았을 때 8비트 CPU를 사용했었는데 그때에 비하면 8배가 커진 셈인데, 실제로는 그보다 훨씬 더 용량도 커지고 계산도 빨라졌어. 그 덕분에 요즘의 실감나는 게임도 만들어지는 거임ㅋㅋ. 비트라는 단위가 워낙 크기가 작기 때문에 2진수 8개가 모인 8비트를 1바이트(Byte)라고 하고, 일반적으로 바이트라는 단위를 많이 사용하지.
데이터 형(Data Types)
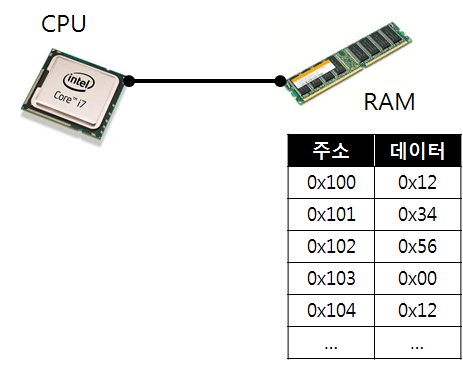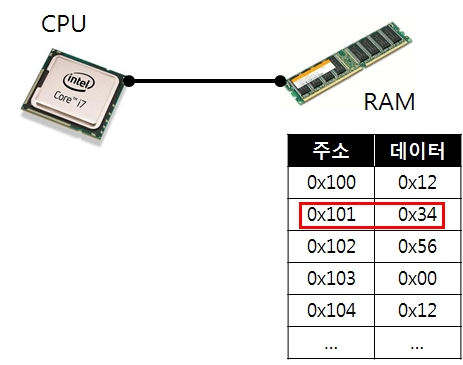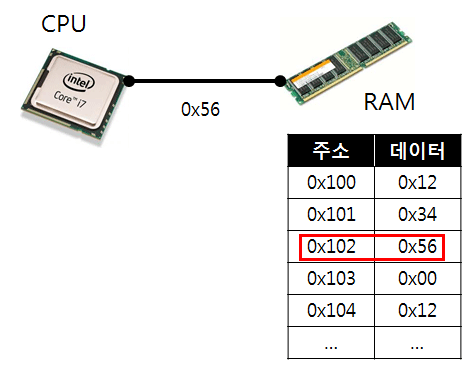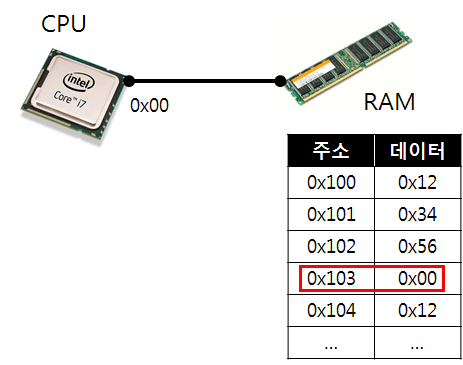
자, 이제 프로그래밍의 기본적인 부분에 대해 알아보자. 컴퓨터로 프로그램을 만들어서 할 수 있는 게 무엇일 까 생각해보자. 우리가 자주 쓰는 프로그램들이 무엇이 있을까? 계산기, 게임, 워드프로세서, 게임, 인터넷, 게임, 등등이 있는 데 모든 프로그램은 결국은 아래 그림의 3가지 단계로 일을 하는 것을 알 수 있어.
어떤 정보(데이터 혹은 명령어)를 입력하고, 이에 대해 처리하고, 그 결과를 출력하는 3가지 단계이지. 그렇다면 입력, 처리, 출력하는 정보들은 도대체 실제로는 어떤 것일까?
정답은 이 글의 제목에 써 놓았는데 전부 다 숫자라는 점을 알아야 해. 그리고 또 그 숫자는 내부적으로 2진수로 되어있는 것이지. 하지만 프로그램을 만들 때 0과 1만 가지고 입력시키고 또 그 결과를 출력해 보면 사람이 알아볼 수가 없어. 매트릭스라는 유명한 영화를 보면 함선에 타고 있는 기술자들은 화면에 이상한 글자들이 쏟아져 내려오는 것을 보고 주인공이 위험에 빠져있다는 얘기를 하는 장면이 나오는데 굳이 말하자면 그 사람은 숫자만 보고 그것이 의미하는 글자나 그림으로 바로 해석을 할 수 있다는 뜻이 돼. 정말 좋겠다.
아무리 숫자라고 하더라도 2진수만으로는 할 수 없기 때문에 실제 프로그램에서는 10진수 혹은 16진수를 사용하고, 또 8비트 컴퓨터라고 255까지만 계산해주어서는 안되기 때문에 2진수 여러 자리 수를 사용하여 데이터 형(Data Type)이라는 것을 정해 놓았어. 이것은 프로그램 언어마다 조금씩 다른데 프로그램 언어가 무엇인지는 다음 번에 이야기하고, 우리는 C++을 배우려고 하는 것이니까 C++을 기준으로 알려 줄께.
데이터 형 종류
|
명칭
|
비트 수
|
부호 있는 정수(signed integer)
|
char
|
8
|
short
|
16
|
long
|
32
|
부호 없는 정수(unsigned integer)
|
unsigned char
|
8
|
unsigned short
|
16
|
unsigned long
|
32
|
실수(floating point)
|
float
|
32
|
double
|
64
|
복잡해 보이지만 큰 숫자 혹은 정확한 숫자가 필요할 때에는 비트 수가 큰(용량을 많이 차지하는) 데이터 형을 쓰고 반대로 작은 숫자들로만 처리가 가능한 때에는 비트 수가 작은 데이터 형을 쓰게 돼. 컴퓨터 안에 있는 메모리, 디스크와 같이 데이터를 저장하는 곳은 무한정 많은 양을 담을 수 있는 것이 아니고 용량이 정해져 있기 때문에 처리하고자 하는 일이 무엇인 가를 잘 따져서 적합한 데이터 형을 써야 해. 예를 들어 학생들의 과목 별 시험 점수를 처리하고자 할 때는 0점부터 100점까지로 범위가 정해져 있기 때문에 8비트 크기의 정수(char)를 쓰면 충분하다는 거지.
8비트의 숫자는 0에서 255까지를 표현할 수 있다고 했는데, 음수를 넣고 싶으면 어떻게 할 까? 한 가지 방법은 8비트 중에 1개의 비트를 부호(0이면 양수, 1이면 음수)를 결정하는데 사용하고 남은 7비트를 숫자로 쓰면 되겠지. 실제 컴퓨터에서 음수를 표현하는 방법은 조금 다르지만 비슷한데 어찌되었던간에 256가지를 구별할 수 있기 때문에 부호있는 8비트 정수는 -128에서 127까지를 사용해. 점점 복잡해진다@.@ㅋ
아스키 코드(ASCII Code)
숫자에 대해서만 쭉 공부해봤는데 정작 컴퓨터에서 보는 대부분의 정보는 글자로 되어있잖아? 이건 어떻게 하는 걸 까? 옛날 사람들이 이 고민을 다 해서 좋은 것을 만들어 놓았지. 다름 아니라 우리가 쓰는 글자(character)들을 각각 순서를 매긴 다음에 번호를 붙여서 쓰는거야. 컴퓨터를 처음 만든 사람들이 미국 사람들이다 보니 자기들이 쓰는 글자인 영어 알파벳을 가지고 번호를 매겨 놓았고 이것은 기본적으로 지금도 그대로 쓰고 있어. 알파벳이 A부터 Z까지 모두 26개이기 때문에 번호를 붙이는 일이 그리 어렵지 않았지. 이렇게 만들어 놓은 것은 아스키코드(ASCII Code)라고 해. 이름이 이상한데,
American
Standard
Code for
Information
Interchange의 앞 글자를 딴 거야(
자세한 설명).
원래 ASCII 코드는 0에서 127까지로 정해져 있어서 8비트 정수(1바이트) 하나 당 한 글자씩 넣을 수 있어. 쉽게 생각하면 10글자를 저장하는데 10바이트가 필요한 식이지. 그 이후에 영어가 아닌 다른 언어를 쓰는 나라들도 자신의 글자에 맞는 값을 정해서 사용했어. 물론 우리 나라에서도 한글을 표시하기 위해 코드를 정해서 쓰고 있어.
문제
1) 16비트 CPU가 최대로 처리할 수 있는 숫자를 10진수와 16진수로 각각 나타내시오.
2) 위의 아스키코드 표의 코드 숫자는 10진수이다. 다음의 16진수를 ASCII코드 표를 찾아 글자로 바꾸시오.
0x53 0x65 0x61 0x6E 0x20 0x26 0x20 0x52 0x75 0x62 0x69
3) 팔만대장경은 52,330,152개의 한문 글자, 성경은 3,566,400개의 영어 글자로 되어 있다고 한다. 한문 1글자를 기록하는데 2바이트, 영어 1글자를 기록하는데 1바이트가 필요하다고 하면 팔만대장경과 성경을 컴퓨터에 입력하기 위해 각각 얼마의 용량이 필요한가?